【机器学习】
标签:
监督学习
拟合函数
损失函数
梯度下降
机器学习分为【监督学习】和【无监督学习】。我们这里先说监督学习。 监督学习是指你有一些带有已知标签的数据,把这些数据拟合成一个函数,从而可以用这个函数去预测未知的值。 比如:我们有已知的三个值 1、2、3,已知它们的标签为 2、3、4。即 1->2, 2->3, 3->4 那我们怎么预测 5 的标签是多少呢? 这里我们把每个数据作为一个样本点,三个样本点分别为:(1,2) (2, 3) (3, 4) 我们知道可以用 y = kx + b 来表示一条直线,带入以上数值,解出 k=1, b=1, 即 y = x + 1 把 x = 5 带入直线,解得 y = 6,就成功预测了 5 的标签为 6
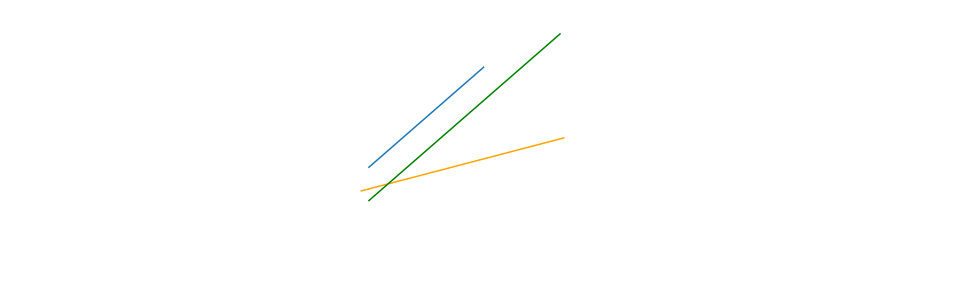
那么问题来了,现实生活中的真实值大多时候不会这么完美的落到一条直线上, 比如:我们的值是这样的(1, 2) (2, 2.8) (3, 4.2) 那怎么办呢?我们就找一个能尽可能多的靠近所有点的直线,使误差达到最小,如图五,我们可以看出,中间的绿色直线是最好的一条直线,我们怎么找到这样一条直线呢?
我们先从最简单的情况开始,假设三个样本点为(1, 1) (2, 1.8) (3., 3.2)如图六:
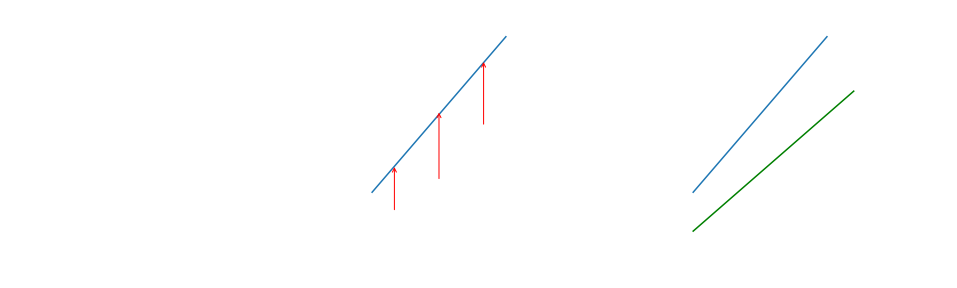
假设函数 y = kx,在机器学习中我们经常这么表示假设函数:这里引出一个概念“损失函数”,损失函数就是每个样本点到我们的直线的距离的总和。我们容易看出,当损失函数最小时,即每个样本点到我们的直线的距离(如图七中的箭头长度)的和最小时就是我们要找的拟合的最好的直线,即图八中绿色的直线。 我们定义损失函数:
怎样使损失函数最小呢? 我们以上面三个样本点为例,代入展开为:
继续展开,为:
化简,得:
我们画出此损失函数的图像为:

我们发现,损失函数其实是一个开口向上的抛物线,我们知道抛物线的顶点是其最小值,即图中的红点。 红点即为其导数为0的点,损失函数的导数为:令其等于0,解得:

我们解出最小值为我们求出最小值时k和b的值,即y=x+b
python代码:
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
import time
#from mpl_toolkits.mplot3d import Axes3D
#from decimal import Decimal
#from fractions import Fraction
# 线性回归
class LinearRegression:
def __init__(self, x_points, y_points):
self.X = np.array(x_points)
self.Y = np.array(y_points)
self.point_size = len(x_points)
# ================= 用户自定义参数 =====================
self.SLEEP_TIME = 0.001 # 动画间隔时间
self.STEP_ALPHA = 0.1 # 梯度下降的步长
self.show_view = True # 是否可视化显示
# =================== 画布设置 =======================
_fig = plt.figure(figsize=(13.3, 5)) # 设置画布大小
mngr = plt.get_current_fig_manager() # 获取当前figure manager
mngr.window.wm_geometry("+10+110") # 调整窗口在屏幕上弹出的位置
plt.subplots_adjust(left=0.05, right=0.98, bottom=0.1, top=0.8) # 设置子图的边距
plt.ion()#打开交互模式
#plt.subplots_adjust(left=0.2, bottom=0.2, right=0.8, top=0.8, hspace=0.2, wspace=0.3)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# ==================== 子图 ========================
#self.ax1 = plt.subplot(1, 2, 1) # 子图1
#self.ax2 = plt.subplot(1, 2, 2) # 子图2
self.ax1 = _fig.add_subplot(131) # 子图1
plt.title('拟合数据点')
self.ax1.set_xlabel('x label', color='r')
self.ax1.set_ylabel('y label', color='g')
# self.ax2 = _fig.add_subplot(122) # 子图2
self.ax2_3d = _fig.add_subplot(132, projection='3d') # 3维子图
self.ax2_3d.set_title('平方差损失函数')
self.ax2_3d.set_xlabel('x label', color='r')
self.ax2_3d.set_ylabel('y label', color='g')
self.ax2_3d.set_zlabel('z label', color='b')
# θ散点图
self.ax3 = _fig.add_subplot(133)
self.ax3.set_title('θ值')
self.ax3.set_xlabel('upte times', color='r')
self.ax3.set_ylabel('θ值', color='g')
# self.theta = 0 # 梯度下降的初始值
self.theta0 = 0
self.theta1 = 0
#self.power2, self.power1, self.power0 = self.analysis_cost_function(x_points, y_points)
# =================== 函数系数初始化 ===================
# 多项式系数
self.theta0_power2 = 0
self.theta1_power2 = 0
self.theta0_theta1 = 0
self.theta0_power1 = 0
self.theta1_power1 = 0
self.power0 = 0
# θ0的微分函数系数
self.iteration_theta0_0 = 0
self.iteration_theta0_1 = 0
self.iteration_theta0_2 = 0
# θ1的微分函数系数
self.iteration_theta1_0 = 0
self.iteration_theta1_1 = 0
self.iteration_theta1_2 = 0
# 预处理,解析函数,求多项式系数
self.__analysis_cost_function(x_points, y_points)
# 展示回归过程
def regression0(self):
# 绘制散点图
self.ax1.scatter(self.X, self.Y)
plt.pause(self.SLEEP_TIME)
# 绘制抛物线
X1 = np.linspace(0, 2, 30, endpoint=True)
self.ax2.plot(X1, self.__get_power2_y(X1))
plt.pause(self.SLEEP_TIME)
# 梯度下降法拟合函数
self.__show_current_theta_line0(self.theta)
old = self.theta
while True:
self.theta = self.theta - self.STEP_ALPHA * (1 / (self.point_size)) * self.__get_dx()
self.__show_current_theta_line0(self.theta)
if self.theta == old:
break
old = self.theta
print(f'结束,收敛于:{old}')
# 展示回归过程
def regression(self, show_view=True):
self.show_view = show_view
if self.show_view:
# 绘制散点图
self.ax1.scatter(self.X, self.Y)
plt.pause(self.SLEEP_TIME)
# 绘制代价函数三维图
X1 = np.linspace(-1.3, 1.2, 100, endpoint=True)
X2 = np.linspace(-0.3, 2.5, 100, endpoint=True)
X1, X2 = np.meshgrid(X1, X2)
Z = self.__get_power2_y(X1, X2)
self.ax2_3d.plot_surface(X1, X2, Z, alpha=0.7)
plt.pause(self.SLEEP_TIME)
theta0_old = self.theta0
theta1_old = self.theta1
last_abvious_change0 = self.theta0
last_abvious_change1 = self.theta1
last_abvious_change0_1 = self.theta0
last_abvious_change1_1 = self.theta1
update_times = 0
# 梯度下降法拟合函数
print(f'第{update_times}次梯度下降,当前θ值为:θ0: {self.theta0}, θ1: {self.theta1}')
self.__show_current_theta_line(self.theta0, self.theta1)
self.__show_current_theta_value(update_times, self.theta0, self.theta1)
while True:
update_times += 1
# 梯度下降法更新参数
tmp0 = self.theta0 - self.get_dx_theta0()
tmp1 = self.theta1 - self.get_dx_theta1()
self.theta0 = tmp0
self.theta1 = tmp1
print(f'第{update_times}次梯度下降,当前θ值为:θ0: {self.theta0}, θ1: {self.theta1}')
# 有明显变化时才绘制
if abs(self.theta0 - last_abvious_change0) > 0.1 or abs(self.theta1 - last_abvious_change1) > 0.1:
self.__show_current_theta_line(self.theta0, self.theta1)
last_abvious_change0 = self.theta0
last_abvious_change1 = self.theta1
if abs(self.theta0 - last_abvious_change0) > 0.1 or abs(self.theta1 - last_abvious_change1) > 0.1:
self.__show_current_theta_value(update_times, self.theta0, self.theta1)
last_abvious_change0_1 = self.theta0
last_abvious_change1_1 = self.theta1
elif update_times % 30 == 0:
self.__show_current_theta_value(update_times, self.theta0, self.theta1)
#self.__show_current_theta_value(update_times, self.theta0, self.theta1)
'''
if update_times % 30 == 0:
self.__show_current_theta_value(update_times, self.theta0, self.theta1)
last_abvious_change0_1 = self.theta0
last_abvious_change1_1 = self.theta1
'''
# 如果找到最小值结束迭代
if self.theta0 == theta0_old and self.theta1 == theta1_old:
print('精确收敛,结束')
break
# 如果变化特别特别微小,结束迭代
if abs(self.theta0-theta0_old) < 1e-8 and abs(self.theta1-theta1_old) < 1e-8:
print('更新值差值小于1e-8,结束')
break
theta0_old = self.theta0
theta1_old = self.theta1
print(f'最终收敛, θ0收敛于: {self.theta0}, θ1收敛于: {self.theta1}')
# 消除小数运算误差
fixed1 = abs(self.theta0-round(self.theta0)) < 1e-5
fixed2 = abs(self.theta1-round(self.theta1)) < 1e-5
if fixed1:
self.theta0 = round(self.theta0)
if fixed2:
self.theta1 = round(self.theta1)
if fixed1 or fixed2:
print(f'消除误差后,θ0收敛于: {self.theta0}, θ1收敛于: {self.theta1}')
# 绘图显示最终的结果
self.__show_current_theta_line(self.theta0, self.theta1, color='r')
# 解析函数
def analysis_cost_function0(self, x_points, y_points):
power2, power1, power0 = 0, 0, 0
for i, x in enumerate(x_points):
power2 += x**2
power1 += -2 * x * y_points[i]
power0 += y_points[i] ** 2
_2m_1 = 1 / (2 * len(x_points))
power2 *= _2m_1
power1 *= _2m_1
power0 *= _2m_1
print(f'平方差代价函数为: {power2}θ^2{"+" if power1 >= 0 else ""}{power1}θ{"+" if power0 >= 0 else ""}{power0}')
print(f'导数为: {2*power2}θ{"+" if power1 >= 0 else ""}{power1}')
return power2, power1, power0
# 预处理,解析函数,求多项式系数
def __analysis_cost_function(self, x_points, y_points):
self.theta0_power2 = len(x_points) # θ0^2 的系数
self.iteration_theta0_0 = len(x_points)
for i, x in enumerate(x_points):
# 解析代价函数多项式参数
self.theta1_power2 += x**2 # θ1^2 的系数
self.theta0_theta1 += 2 * x # θ0*θ1 的系数
self.theta0_power1 += -2 * y_points[i] # θ0 的系数
self.theta1_power1 += -2 * x * y_points[i] # θ1 的系数
self.power0 += y_points[i] ** 2 # 常数项
# 计算偏微分函数多项式参数
self.iteration_theta0_1 += x
self.iteration_theta0_2 += -y_points[i]
self.iteration_theta1_0 += x
self.iteration_theta1_1 += x**2
self.iteration_theta1_2 += -x * y_points[i]
str1 = f'平方差损失函数为: 1/{2*len(x_points)}({self.theta0_power2}θ0^2 {"+" if self.theta1_power2 >= 0 else "-"} {abs(self.theta1_power2)}θ1^2 {"+" if self.theta0_theta1 >= 0 else "-"} {abs(self.theta0_theta1)}θ0θ1 {"+" if self.theta0_power1 >= 0 else "-"} {abs(self.theta0_power1)}θ0 {"+" if self.theta1_power1 >= 0 else "-"} {abs(self.theta1_power1)}θ1 {"+" if self.power0 >= 0 else "-"} {abs(self.power0)})'
str2 = f'导数为: 1/{2*len(x_points)}({2*self.theta0_power2}θ0 {"+" if self.theta1_power2 >= 0 else "-"} {abs(2*self.theta1_power2)}θ1 {"+" if self.theta0_theta1 else "-"} {abs(self.theta0_theta1)})'
str3 = f'θ0偏微分函数为: 1/{len(x_points)}({self.iteration_theta0_0}θ0 {"+" if self.iteration_theta0_1 >= 0 else "-"} {abs(self.iteration_theta0_1)}θ1 {"+" if self.iteration_theta0_2 >= 0 else "-"} {abs(self.iteration_theta0_2)})'
str4 = f'θ1偏微分函数为: 1/{len(x_points)}({self.iteration_theta1_0}θ0 {"+" if self.iteration_theta1_1 >= 0 else "-"} {abs(self.iteration_theta1_1)}θ1 {"+" if self.iteration_theta1_2 >= 0 else "-"} {abs(self.iteration_theta1_2)})'
# 乘以 1/2m
_2m_1 = 1 / (2 * len(x_points))
self.theta0_power2 *= _2m_1
self.theta1_power2 *= _2m_1
self.theta0_theta1 *= _2m_1
self.theta0_power1 *= _2m_1
self.theta1_power1 *= _2m_1
self.power0 *= _2m_1
# 乘以 1/m
_m_1 = 1 / len(x_points)
self.iteration_theta0_0 *= _m_1
self.iteration_theta0_1 *= _m_1
self.iteration_theta0_2 *= _m_1
self.iteration_theta1_0 *= _m_1
self.iteration_theta1_1 *= _m_1
self.iteration_theta1_2 *= _m_1
# 绘图界面上显示解析出来的多函数
if self.show_view:
self.ax2_3d.set_title(f'{str1}\n{str2}\n{str3}\n{str4}', fontsize='x-small', horizontalalignment='left', loc='left')
# 输出解析出来的函数
print(str1)
print(str2)
print(str3)
print(str4)
# θ0的微分函数
def get_dx_theta0(self):
#return self.STEP_ALPHA * (1/self.point_size) * (3*self.theta0+6*self.theta1-9)
#return Decimal(f'{self.STEP_ALPHA}') * (Decimal(f'{1}')/Decimal(f'{self.point_size}')) * (Decimal(f'{3}')*Decimal(f'{self.theta0}')+Decimal(f'{6}')*Decimal(f'{self.theta1}')-Decimal(f'{9}'))
return self.STEP_ALPHA * (1/self.point_size) * (self.iteration_theta0_0*self.theta0+self.iteration_theta0_1*self.theta1+self.iteration_theta0_2)
# θ1的微分函数
def get_dx_theta1(self):
#return self.STEP_ALPHA * (1/self.point_size) * (6*self.theta0+14*self.theta1-20)
#return Decimal(f'{self.STEP_ALPHA}') * (Decimal(f'{1}')/Decimal(f'{self.point_size}')) * (Decimal(f'{6}')*Decimal(f'{self.theta0}')+Decimal(f'{14}')*Decimal(f'{self.theta1}')-Decimal(f'{20}'))
return self.STEP_ALPHA * (1/self.point_size) * (self.iteration_theta1_0*self.theta0+self.iteration_theta1_1*self.theta1+self.iteration_theta1_2)
# 代价函数
def __get_power2_y0(self, x):
#return (1/(2*self.point_size))*self.power2*x**2 + (1/(2*self.point_size))*self.power1*x + (1/(2*self.point_size))*self.power0 # 14x^2 - 28.4x + 14.48
pass#return self.power2*x**2 + self.power1*x + self.power0 # 14x^2 - 28.4x + 14.48
# 代价函数
def __get_power2_y(self, theta0, theta1):
return self.theta0_power2*theta0**2 + self.theta1_power2*theta1**2 + self.theta0_theta1*theta0*theta1 + self.theta0_power1*theta0 + self.theta1_power1*theta1 + self.power0
# 导数
def __get_dx0(self):
#return (1/(2*self.point_size))*self.power2*2*self.theta + (1/(2*self.point_size))*self.power1
return 2*self.power2*self.theta + self.power1
# 导数
def __get_dx(self):
return 2*self.theta0_power2*self.theta0 + 2*self.theta1_power2*self.theta1 + self.theta0_theta1 + self.theta0_power1 + self.theta1_power1
# 绘制出theta点和当theta为此值时拟合出来的直线
def __show_current_theta_line0(self, theta):
print(f'梯度下降,当前θ值为:{theta}')
# 绘制切线处的点
plt.sca(self.ax2)
plt.scatter(theta, self.__get_power2_y0(theta))
plt.pause(self.SLEEP_TIME)
# 绘制一次函数
plt.sca(self.ax1)
plt.plot(self.X, theta*self.X)
plt.pause(self.SLEEP_TIME)
# 绘制出theta点和当theta为此值时拟合出来的直线
def __show_current_theta_line(self, theta0, theta1, color=None):
if not self.show_view:
return
# ================ 绘制梯度下降的点 ==================
self.ax2_3d.scatter3D(theta0, theta1, self.__get_power2_y(theta0, theta1), color='r')
#plt.pause(self.SLEEP_TIME)
# ================ 绘制拟合的一次函数 ================
# 清除上次的绘制
if self.ax1.lines:
self.ax1.lines.pop(0)
#self.ax1.lines.remove(self.ax1.lines[0])
#del self.ax1.lines
#self.ax1.clear()
#self.ax1.cla()
# 绘制
if color is None:
self.ax1.plot(self.X, theta0+theta1*self.X, alpha=0.5)
else:
self.ax1.plot(self.X, theta0+theta1*self.X, color=color)
self.ax1.set_title(f'当前拟合结果为: y = {theta0:.1f} + {theta1:.1f}x')
plt.pause(self.SLEEP_TIME)
# 绘制θ值
#self.ax3.scatter(theta0, theta1)
#plt.pause(self.SLEEP_TIME)
def __show_current_theta_value(self, update_times, current_theta0, current_theta1):
if not self.show_view:
return
self.ax3.scatter(update_times, current_theta0, color='r', alpha=0.5)
self.ax3.scatter(update_times, current_theta1, color='g', alpha=0.5)
plt.pause(self.SLEEP_TIME)
if __name__ == '__main__':
#line_regression = LinearRegression([0, 1, 2, 3], [0, 0.8, 2.2, 3.0])
#line_regression = LinearRegression([0, 1, 2, 3, 4, 5], [0, 1.8, 4.2, 5.8, 8.2, 10])
#line_regression = LinearRegression([0, 1, 2, 3, 4, 5], [0, 1, 2, 3, 4, 5])
#line_regression = LinearRegression([0, 1, 2, 3], [1, 2, 3, 4])
#line_regression = LinearRegression([1, 2, 3], [2, 3, 4])
line_regression = LinearRegression([1, 2, 3], [1, 2, 3])
line_regression.regression()
运行效果:
